Model Reduction Software
Name
emgr - EMpirical GRamian framework for (nonlinear) input-output systems.
Description
System gramians are matrices associated to linear input-output systems and quantify their controllability, observability and minimality.
Empirical system gramian matrices (empirical gramians) are a generalization computable for linear but also for parametric and nonlinear (state-space) systems and have, among others (see below), applications in model order reduction.
Model reduction via empirical gramians is applicable to the state-space, to the parameter-space or both, through combined state and parameter reduction.
For state reduction, the empirical reachability gramian / empirical controllability gramian and the empirical observability gramian, or the empirical cross gramian (the empirical linear cross gramian for large-scale linear systems) are available.
For sensitivity analysis, parameter identification, and parameter reduction, the empirical sensitivity gramian (controllability of parameters), or the empirical identifiability gramian and empirical cross-identifiability gramian (observability of parameters) are provided.
Combined reduction is enabled by the empirical joint gramian, which computes minimality of states (via the cross gramian) and observability of parameters (via the cross-identifiability gramian) simultaneously.
Furthermore, the empirical output reachability gramian / empirical output controllability gramian is computable.
Overall, empirical system Gramians are an advanced data-driven system-theoretic method and a numerical tool for GRAMIAN-based (non)linear input-output system analysis.
The empirical gramian framework — emgr — is a compact open-source toolbox,
compatible with OCTAVE and MATLAB,
that provides a unified interface for unsupervised learning of system-theoretic operators from small data.
Scope

- Model Order Reduction (MOR) | Model Reduction
- Parametric Model Order Reduction (pMOR) | Robust Reduction
- Nonlinear Model Order Reduction (nMOR)
- Parameter Reduction
- Combined State and Parameter Reduction (Combined Reduction)
- Decentralized Control | Control Configuration Selection
- Sensitivity Analysis
- Parameter Identification | Input-Output Identifiability
- Nonlinearity Quantification
- Uncertainty Quantification
- System Norms | System Indices | System Invariants
- Optimal Sensor Placement | Optimal Actuator Placement
- Matrix Equations
Download
Get emgr here: emgr.m (Version: 5.99, CRC32: f76f4638)
[emgr-5.99.zip]
[mirror]
[source]
[meta]
[repo]
(emgr is written in the Matlab programming language and requires Octave >= 5.2 or MATLAB >= 2017b, yet emgr has no dependencies on toolboxes or packages.)
License
All source code is licensed under the open source BSD-2-Clause license:
Copyright (c) 2013–2022, Christian Himpe
All rights reserved.
Redistribution and use in source and binary forms, with or without
modification, are permitted provided that the following conditions are met:
1. Redistributions of source code must retain the above copyright notice, this
list of conditions and the following disclaimer.
2. Redistributions in binary form must reproduce the above copyright notice,
this list of conditions and the following disclaimer in the documentation
and/or other materials provided with the distribution.
THIS SOFTWARE IS PROVIDED BY THE COPYRIGHT HOLDERS AND CONTRIBUTORS "AS IS" AND
ANY EXPRESS OR IMPLIED WARRANTIES, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED
WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR PURPOSE ARE
DISCLAIMED. IN NO EVENT SHALL THE COPYRIGHT OWNER OR CONTRIBUTORS BE LIABLE FOR
ANY DIRECT, INDIRECT, INCIDENTAL, SPECIAL, EXEMPLARY, OR CONSEQUENTIAL DAMAGES
(INCLUDING, BUT NOT LIMITED TO, PROCUREMENT OF SUBSTITUTE GOODS OR SERVICES;
LOSS OF USE, DATA, OR PROFITS; OR BUSINESS INTERRUPTION) HOWEVER CAUSED AND
ON ANY THEORY OF LIABILITY, WHETHER IN CONTRACT, STRICT LIABILITY, OR TORT
(INCLUDING NEGLIGENCE OR OTHERWISE) ARISING IN ANY WAY OUT OF THE USE OF THIS
SOFTWARE, EVEN IF ADVISED OF THE POSSIBILITY OF SUCH DAMAGE.
Disclaimer
This is research software!
Model
The target mathematical model is a general input-output system (aka control system):
ẋ(t) = f(x(t),u(t),p,t)
y(t) = g(x(t),u(t),p,t)
consisting of a first-order ordinary differential equation (ODE) with vector field f and an algebraic output function g,
of which either (may) depend on input u(t), state x(t), parameter p and time t, yielding the output y(t).
This model maps an input (control) to an output (quantities of interest) via the state evolving under a dynamical system.
Algorithm
The computation of empirical system Gramians is described in the open-access article:
C. Himpe; "emgr -- the Empirical Gramian Framework"; Algorithms, 11(7): 91, 2018;
and references therein.
Usage
General Usage: W = emgr(f,g,s,t,w,pr,nf,ut,us,xs,um,xm,dp);
Minimal Usage: W = emgr(f,g,s,t,w);
About Info Usage: v = emgr('version');
Mandatory Arguments
f- handle to a function with signaturex = f(x,u,p,t), the system's vector field,g- handle to a function with signaturey = g(x,u,p,t), the system's output functional;g = 1impliesy = x,s- three component vectors = [M,N,Q]holding number of inputs (M), states (N) and outputs (Q),t- two component vectort = [dt,Tf]holding time step (dt) width and time horizon (Tf),w- a character selecting the gramian type (For details see Gramians).
Optional Arguments
pr- System's parameters (Default:0;'s','i','j'require two columns for min and max parameter),vector- column vector holding the parameters,matrix- set of column vectors holding different sets of parameters.
nf- Thirteen component vector holding options; (Default:0, for details see Option Flags).ut- Input time series (Default:'i'),handle- handle to function with signatureu_t = ut(t),'i'- delta impulse input,'s'- step input / load vector / source term,'h'- decaying exponential chirp input via havercosine,'a'- cardinal sine / sinc input,'r'- uniformly random binary input.
us- Steady-state input (Default:0),scalar- sets allMinput components to provided value,vector- steady-state input column vector of dimensionM.
xs- Steady-state, also nominal initial state (Default:0),scalar- sets allNsteady-state components to provided value,vector- steady-state column vector of dimensionN.
um- Input perturbation scales (Default:1),scalar- set all maximum scales to argument,vector- set maximum to scale to argument,matrix- set scales to argument, used as is.
xm- Initial state perturbation scales (Default:1),scalar- set all maximum scales to argument,vector- set maximum to scale to argument,matrix- set scales to argument, used as is.
dp- Custom inner product handlexy = dp(x,y)(Default:@mtimes).
Gramian Types
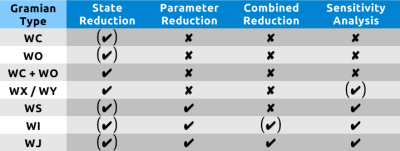
'c'- Empirical Controllability Gramian (WC),'o'- Empirical Observability Gramian (WO),'x'- Empirical Cross Gramian (WXsometimes noted asWCO),'y'- Empirical Linear Cross Gramian (WY),'s'- Empirical Sensitivity Gramian (WS, controllability of parameters),'i'- Empirical Identifiability Gramian (WI, observability of parameters, via augmented observability Gramian),'j'- Empirical Joint Gramian (WJ, observability of parameters via cross-identifiability Gramian).
Option Flags
nf(1)- Center time series around (Default:0),= 0- zero (balanced POD),= 1- steady-state (empirical covariances),= 2- final state,= 3- arithmetic average over time (empirical gramians),= 4- root-mean-square over time,= 5- mid-range over time.
nf(2)- Input scale sequence (Default:0),= 0- singleum = um;= 1- linearum = um * [0.25, 0.50, 0.75, 1.0];= 2- geometricum = um * [0.125, 0.25, 0.5, 1.0];= 3- logarithmicum = um * [0.001, 0.01, 0.1, 1.0];= 4- sparseum = um * [0.01, 0.5, 0.99, 1.0];
nf(3)- State scale sequence (Default:0),= 0- singlexm = xm;= 1- linearxm = xm * [0.25, 0.50, 0.75, 1.0];= 2- geometricxm = xm * [0.125, 0.25, 0.5, 1.0];= 3- logarithmicxm = xm * [0.001, 0.01, 0.1, 1.0];= 4- sparsexm = xm * [0.01, 0.5, 0.99, 1.0];
nf(4)- Input transformations (Default:0),= 0- unitum = [-um, um];= 1- singleum = um;
nf(5)- State transformations (Default:0),= 0- unitxm = [-xm, xm];= 1- singlexm = xm;
nf(6)- Gramian normalization, onlyWC, WO, WX, WY(Default:0),= 0- no normalization,= 1- normalize with Jacobi preconditioner,= 2- normalize with steady-state (input).
nf(7)- State gramian variant (Default:0),= 0- regular,= 1- output-controllability gramian (WC, WS),= 1- averaged observability gramian (WO, WI),= 1- non-symmetric cross gramian (cross operatorWZ) for non-square, non-symmetric or non-gradient systems (WX, WY, WJ).
nf(8)- Enable nominal input during parameter and state perturbations, onlyWO, WX, WS, WI, WJ(Default:0),= 0- no extra input,= 1- extra input for state or parameter perturbations.
nf(9)- Parameter centering and scale sequence, onlyWS, WI, WJ(Default:0),= 0- no centering and linear scales,= 1- linear centering and scales,= 2- logarithmic centering and scales.= 3- nominal centering and scales.
nf(10)- Parameter gramian variant, onlyWS, WI, WJ(Default:0),= 0- input-state average (WS),= 1- input-output average (WS),= 0- coarse Schur-complement (WI, WJ),= 1- approximate Schur-complement (WI, WJ).= 2- exact Schur-complement (WI, WJ).
nf(11)- Cross gramian partition width, onlyWX, WJ(Default:0),= 0- full cross Gramian, no partitioning,< N- maximum partition width.
nf(12)- Partitioned cross gramian running index, onlyWX, WJ(Default:0),= 0- no partitioning,> 0- index of cross gramian partition to be computed.
nf(13)- Weight time series (Default:0),= 0- one (no weighting),= 1- linear time-weighting,= 2- quadratic time-weighting,= 3- state-based weighting,= 4- scale-based weighting.= 5- reciprocal square-root time-weighting.
Return Values
- State-space empirical gramian matrix (for:
WC, WO, WX, WY). - Cell array of state-space and parameter-space empirical gramian matrix (for:
WS, WI, WJ).
Solver Interface
ODE.
- Function signature:
y = solver(f,g,t,x0,u,p)f- handle to a function with signaturex = f(x,u,p,t), the system's vector field,g- handle to a function with signaturey = g(x,u,p,t), the system's output functional,t- two component vectort = [dt,Tf]holding time step width (dt) and time horizon (Tf),x0- column vector of dimensionNholding initial state,u- handle to function with signatureu_t = u(t),p- column vector holding (current) parameter(s).
- Included default solver: SSPx2
- Explicit Second Order Runge-Kutta (RK2)
- Optimal Strong Stability Preserving (SSP)
- Low-Storage implementation
- Configurable number of stages via global variable
STAGESfor enhanced stability (Default:STAGES = 3) STAGES = 1induces the Euler Method (first order explicit Runge-Kutta)STAGES = 2induces the Heun's Method (second order explicit Runge-Kutta)- From "Highly Efficient Strong Stability-Preserving Runge–Kutta Methods with Low-Storage Implementations" by D.I. Ketcheson (2008)
Empirical System Theory
The platform est.m prototypically enables testing and evaluating methods based on empirical gramians.est has the following capabilities:
- Model reduction (POD, DSPMR, Modified POD, bPOD, BT, DMD-Galerkin)
- Parameter reduction
- Combined state and parameter reduction
- Decentralized control (RGA, Input-output coherence, DIOPM, H2, SOCI, H∞, PM, HIIA)
- State sensitivity
- Parameter sensitivity
- Parameter identification
- Uncertainty quantification
- Nonlinearity quantification
- Gramian indices
- System indices
- Approximate system norms (H2, H∞, HSH, Ha)
- Matrix equations (Lyapunov, Sylvester)
- Tau function (Inverse spectral problem for Schrödinger's equation)
Minimal Example
A = -0.5*eye(4) % System matrix
B = [0;1;0;1] % Input matrix
C = [0,0,1,1] % Output matrix
WX = emgr(@(x,u,p,t) A*x + B*u, @(x,u,p,t) C*x,[1,4,1],[0.1,10.0],'x') % ≈ B*C
Tests
Tests are defined in emgrTest.m and are evaluated usingest.
The tests are performed on a time-invariant, linear, state-space symmetric MIMO system and optional linear parametrization:
ẋ = A*x + B*u + F*p
y = C*x
Demos
The demo codes can be found in estDemo.m and are evaluated usingest.
Combined Reduction: Nonlinear System (
|
|
Benchmark: Inverse Sylvester Procedure (
|
|
Benchmark: Flexible Space Structures (
|
|
Benchmark: Nonlinear Model Reduction (
|
|
Quadratic Output: Kernel Matrix (
|
|
DMD-Galerkin: All-Pass System (
|
|
PDE Reduction: Advection Equation (
|
|
Nonlinear Second Order Reduction: 5-body Choreography (
|
|
Sensitivity Analysis: Stable Orbits Inside Black Holes (
|
|
About
A gram matrix or gramian matrix W is the result of all inner products of a set of vectors V = [v1 ... vn], in other words: W = VT V,
and closely related to covariance matrix as well as cross-covariance matrix, correlation matrix or cross-correlation matrix respectively.
Properties of (linear) control systems can be assessed by the system gramians,
which are based on the controllability and observability operators.
Classically, the controllability gramian and observability gramian are utilized in balancing model reduction methods.
The cross gramian is not gramian matrix,
but encodes controllability and observability information, and thus minimality, into a single matrix.
Overall, system gramians quantifiy the system-theoretic properties controllability (reachability), observability and (structural) identifiability.
Empirical gramians extend this approach to nonlinear control systems and thus enable nonlinear model reduction. For linear systems, these empirical system gramians are equal to the classic system gramians, yet, empirical gramians are also computable for parametric and nonlinear systems. Furthermore, empirical gramians contain more information about the underlying system; and particularly the empirical cross gramian conveys even additional information. This makes empirical system gramians a versatile tool for mathematical system theory, control theory or computational science and engineering (CSE).
The (discrete) empirical cross gramian encloses information on the input-output behavior of the associated control system as well as approximate Hankel Singular Values and can be computed very efficiently. For large-scale linear systems, the linear empirical cross gramian, related to balanced POD, can be utilized. And for parametric systems, the (empirical) joint gramian, derived from the cross gramian, is available for combined reduction. In case of custom training input, instead of an empirical gramian matrix, an empirical covariance matrix can also be computed.
Model order reduction or short model reduction is an active research field in scientific computing and CSE, which investigates the algorithmic construction of low-order surrogate models for high-dimensional differential equation models. The resulting reduced order models allow a substantially more economical evaluation in terms of computational or memory resources compared to the original large-scale full order model. This numerical model reduction is essential, as developments in computing technology are constantly outpaced by the requirements for model simulation in dimensionality or complexity.
A primary application of empirical Gramians is data-driven model reduction of nonlinear input-output systems. In the language of data science, a nonlinear input-output system corresponds to a recurrent neural network, i.e. from (data-driven) system identification, which can also be (empirical) Gramian-based, or mathematical modeling. Empirical-Gramian-based model reduction then translates to unsupervised learning, where the empirical Gramians encode the network's reducibility based on dynamic behavior induced by systematic perturbations, correlating to synthetic data, and based on a model making it physics-informed.
References
- C. Himpe: "emgr - EMpirical GRamian Framework Version 5.99"; Transactions on Mathematical Software, 49(3): 31, 2023.
- C. Himpe: "Comparing (Empirical-Gramian-Based) Model Order Reduction Algorithms"; in: Model Reduction of Complex Dynamical Systems: 141–164, 2021.
- P. Benner, C. Himpe: "Cross-Gramian-Based Dominant Subspaces"; Advances in Computational Mathematics 45(5): 2533–2553, 2019.
- Synopsis: Extension of the DSPMR method to empirical dominant subspaces using the (empirical) cross gramian.
- Links: self-archived, source, runmycode
- S. Grundel, C. Himpe, J. Saak: "On Empirical System Gramians"; in: Proceedings in Applied Mathematics and Mechanics, 19: e201900006, 2019.
- Synopsis: A brief summary of empirical Gramians and an their application to hyperbolic systems.
- Links: self-archived, source, runmycode
- C. Himpe: "emgr -- the Empirical Gramian Framework"; Algorithms, 11(7): 91, 2018.
- Synopsis: Mathematical and technical documentation of the empirical Gramian framework detailing all features and capabilities.
- Links: self-archived, source, runmycode
- C. Himpe, T. Leibner, S. Rave, J. Saak: "Fast Low-Rank Empirical Cross Gramians"; in: Proceedings in Applied Mathematics and Mechanics, 17: 841–842, 2017.
- C. Himpe, M. Ohlberger: "Cross-Gramian-Based Model Reduction: A Comparison"; in: Model Reduction of Parametrized Systems: 271–283, 2017.
- Synopsis: Summary and tests for Sylvester-equation-based cross gramian, empirical linear cross gramian and empirical cross gramian.
- Links: preprint, source-code, runmycode
- C. Himpe, M. Ohlberger: "A note on the cross gramian for non-symmetric systems"; System Science and Control Engineering, 4(1): 199–208, 2016.
- Synopsis: A new cross gramian matrix for non-symmetric, non-gradient and non-square system.
- Links: self-archived, source-code, runmycode
- C. Himpe, M. Ohlberger: "Accelerating the Computation of Empirical Gramians and Related Methods"; at: 5th International Workshop on Model Reduction in Reacting Flows, 2015.
- Synopsis: Numerical performance enhancements for empirical gramians.
- Links: self-archived, source-code
- C. Himpe, M. Ohlberger: "The Empirical Cross Gramian for Parametrized Nonlinear Systems"; in: IFAC-PapersOnLine (Vienna International Conference on Mathematical Modelling), 48(1): 727–728, 2015.
- Synopsis: Use of the empirical cross gramian for parametric model order reduction by averaging.
- Links: source-code, runmycode
- C. Himpe, M. Ohlberger: "Cross-Gramian-Based Combined State and Parameter Reduction for Large-Scale Control Systems"; Mathematical Problems in Engineering, 2014: 843869, 2014.
- Synopsis: Introduction of the empirical cross gramian and the derived joint gramian as well as gramian-based combined reduction.
- Links: self-archived, source-code, runmycode
- C. Himpe, M. Ohlberger: "Model Reduction for Complex Hyperbolic Networks"; in: Proceedings of the European Control Conference: 2739–2743, 2014.
- Synopsis: Cross gramian based model reduction of a time-varying non-symmetric system with application in network cosmology.
- Links: preprint, source-code, runmycode
- C. Himpe, M. Ohlberger: "A Unified Software Framework for Empirical Gramians"; Journal of Mathematics, 2013: 365909, 2013.
- Synopsis: Mathematical background on and implementation of empirical gramians under a common interface.
- Links: self-archived, source-code, runmycode
Contact
Send feedback to: ch@gramian.de
Cite

- Cite as: C. Himpe (2022). emgr — EMpirical GRamian Framework (Version 5.99) [Software].
https://gramian.dedoi:10.5281/zenodo.6457616 - BibTeX:
@MISC{emgr, author={C.~Himpe}, title={{emgr -- EMpirical GRamian Framework} (Version~5.99)}, howpublished={\url{https://gramian.de}}, year={2022}, doi={10.5281/zenodo.6457616}} - DOI: 10.5281/zenodo.6457616 (Version 5.99)
- Except where otherwise noted, content on this site is licensed under a CC BY 4.0 license.
- Last Change: 2023-09-20
Links
- emgr-ref.pdf (
emgrreference card) - emgr-mini.pdf (
emgrsummary slide) - emgr-flyer.pdf (
emgrflyer) - emgr-refs.md (
emgrbibliography) - emgr-poster-2020.pdf (
emgrposter ICERM) - emgr-poster-2019.pdf (
emgrposter ModRed) - emgr-poster-2018.pdf (
emgrposter MATLAB Expo) - emgr-poster-2015.pdf (
emgrposter OctConf) - emgr-poster-2015a.pdf (
emgrposter SIAM CSE) - orms.mfo.de/project@id=345 (
emgrat Oberwolfach References on Mathematical Software) - swmath.org/software/7554 (
emgrat swMATH) - dsweb.siam.org/Software/emgr-empirical-gramian-framework (
emgrat DSweb) - mathworks.com/matlabcentral/fileexchange/40169-emgr-empirical-gramian-framework (
emgrat fileexchange) - archive.softwareheritage.org/browse/origin/directory/?origin_url=https://github.com/gramian/emgr (
emgrat softwareheritage) - hal.archives-ouvertes.fr/hal-02560320 (
emgrat hal) - freshcode.club/projects/emgr (
emgrat freshcode) - www.mpi-magdeburg.mpg.de/csc/software (
emgrat MPI Magdeburg) - uni-muenster.de/AMM/en/ohlberger/software/ (
emgrat WWU Muenster) - 10.1515/9783110499001-013.pdf (
emgrat MOR software chapter of MOR handbook) - modelreduction.org/index.php/Emgr (
emgrat Model Order Reduction Wiki) - morepas.org/software/emgr (
emgrat Model Reduction for Parametrized Systems) - git.io/mtips (Octave / Matlab Snippets)
Notes
- emgr has AUTHORS, README, CHANGELOG, CITATION.cff, CODE, LICENSE, VERSION, RUNME.m files.
- emgr has a special version emgr.py for Python 3.X.
- emgr can compute the empirical cross gramian columnwise, and thus in parallel on distributed memory systems.
- emgr is not explicitly parallelized but multi-core ready by extensive vectorization and implicit parallelization.
- emgr has highlighted loops that qualify for explicit parallelization using
parfor. - emgr's custom dot-product can also be used for GPGPU based matrix multiplication.
- emgr core function consists of a single file and has less than 600 lines of code!
- emgr's empirical gramian quality depends heavily on the specification of the operating region and the solver.
- emgr's default solver can be used externally by calling
emgr('version'), which sets the global variableODEto a handle.
Troubleshooting
- Issue: An empirical gramian contains very large or infinity values.
- Fix: Likely an unstable trajectory, ensure the perturbations (scales) or parameters do not destabilize the system and a suitable ODE solver is used.
- Issue: The linear cross gramian
WYis zero.- Fix: The second argument for the empirical inear cross gramian has to be the system's adjoint vector field, NOT the output functional.
- Issue: The identifiability gramian
WI{2}or cross-identifiability gramianWJ{2}are zero.- Fix: The parameter steady state (initial state) does not excite the system; usually this means setting
xs≠ 0 ornf(8) = 1.
- Fix: The parameter steady state (initial state) does not excite the system; usually this means setting
- Issue: Using
parforresults in a loop-variable error.- Fix: Since
parforcannot handle non-consecutive loop indices, zero scales or zero min/max parameters are not admissible. Constant parameters may be used if they are last in the parameter vector.
- Fix: Since
- Issue: Using
nf(10) = 1yields infinity values in a parameter gramian ('s','i','j').- Fix: The min or max parameter sets likely contain zeros; try shifting parameters.
- Issue: Using
nf(1) = 1with gramians'o','x','i','j'results in wrong results.- Fix: In these configurations the steady-state output
ys = g(xs,us,p(:,k),0)(for allk) is computed, check ifgworks accordingly.
- Fix: In these configurations the steady-state output
- Issue: The joint gramian / cross-identifiability gramian
'j'results in an error when using a Gaussian kernel as custom inner product.- Fix: Due to the memory-efficient computation via non-square intermediate matrices this combination (as well as with any radial kernel) is incompatible.
Frequently Asked Questions
-
Q: What is model order reduction? What is model reduction?
- A: Model order reduction, or short model reduction, is the algorithmic computation of accurate low-dimensional surrogate models from high-dimensional differential-equation models.
-
Q: What are system Gramians?
- A: System gramians are matrices characterizing the associated (linear) input-output system.
-
Q: What are empirical Gramians?
- A: Empirical system Gramians, or short empirical Gramians, are data-driven approximate system Gramians for parametric or nonlinear systems.
-
Q: How are empirical Gramians related to machine learning?
- A: In the language of machine learning, empirical Gramians provide physics-informed unsupervised learning with synthetic data on recurrent neural networks.
-
Q: What is
emgr?- A: The empirical Gramian framework is a backend toolbox to compute empirical system Gramians.
-
Q: Why not just linearize a nonlinear input-output system?
- A: Linearization typically uses a single linearization point, while empirical Gramians practically average multiple linearization points in a custom operating region of the system.
-
Q: Which files do I need for my own project from the
emgr.ziparchive?-
A: Only the
emgr.mfile is needed; all other files are sample code, tests or documentation.
-
A: Only the
See Also
- Model Reduction Routines (Another Empirical Gramian Software; empirical WC and WO only)
- gram (MATLAB Control System Toolbox; linear WC and WO only)
- gram (Octave Control Package; linear WC and WO only)
Category
tl;dr
emgr: Unsupervised learning of I/O system properties for data-driven control.